An Introduction to Practical Modeling of Reservoir Geomechanics for Appraisal and Development

Introduction

The inter-linking or coupling of geosciences with engineering in cross-disciplinary studies has become increasingly popular in recent years. In the context of the Canadian oil and gas industry, this particularly applies to two major areas: (i) hydraulic fracturing based stimulation of unconventional (i.e. tight) reservoirs or shales, and (ii) thermal recovery based extraction from oil sands. In both scenarios, well productivity during the life of a field is strongly dependent on changes in rock properties that occur over time in the near well-bore region as well as within the reservoir. Specific examples of such phenomena are the stress dependent permeability of stimulated reservoir zones (unconventional reservoirs) and the compaction, dilation or fracture driven permeability changes in unconsolidated reservoirs (oil sands) – the latter influenced by both mechanical and thermal stresses. Evaluation of cap-rock integrity is also a critically important part of all oil sands feasibility studies and mandated by regulatory bodies. As a result, geomechanical modeling is now recognized as an essential part of many appraisal and development projects.

In order to more rigorously capture the physics of reservoirs in simulation and forecast studies, various workflows have been developed. Most of these are modular approaches where the outcome of an analysis or interpretation conducted by one professional discipline serves as the starting block in a follow-up analysis by another discipline. In the simplest approach, the inter-linking of disciplines takes the form of a “handover” of results and reports between groups of geoscientists or engineers. At the next level, an exchange of data can take place between toolkits that may otherwise work independently. As an example, a conventional reservoir simulator can generate pressure maps at discrete times for a depletion plan, and the maps may be subsequently used in a stress simulator to compute corresponding time snapshots of reservoir deformation, compaction, subsidence or heave. At the next higher level of sophistication, an unified application tool can be developed where a broad range of interrelationships are addressed within a single user interface. One example is a coupled simulator that combines flow, geo-mechanics and thermal aspects of complex hydraulic fracturing – and estimates stimulated reservoir volumes as a function of injection parameters. Another example is a coupled simulator that models the injection of steam in a SAGD process and estimates, in addition to the extent of steam chambers and recovery volumes, the associated stresses, rock deformations and modes of mechanical failures of the reservoir and caprock. Yet another related example is a workflow that combines flow modeling during well stimulation with geomechanical modeling of rock failure in order to provide a “forward” model of microseismic events and permeability enhancement (Guest and Settari, 2010) which may be compared with measured microseismicity.

Implementation of Coupled Modeling

From a software developer’s perspective, coupled geomechanical and flow modeling can be implemented in various forms. Fully coupled solutions involve simultaneously solving for multiphase flow in the porous reservoir and deformation and stress fields in a larger rock mass including and surrounding the reservoir (i.e. overburden, side-burden and under-burden). This is the most complex and computationally intensive option. The two solutions can be also coupled in a modular manner – where two separate flow and stress simulators communicate during the solution by exchanging variables. How often the exchanges take place and whether they are one-way or back-and-forth lead us to the nomenclature of explicit versus iterative coupling respectively. Settari and Mourits (1994, 1998) showed that the iterative method, when converged, is equivalent to full coupling but can include “less tight” couplings as special cases. Recently Kim et al. (2009) investigated various iterative strategies between flow and stress, and showed that the Settari and Mourits method is always convergent.

The question of what comprises the optimal degree of coupling does not have a unique answer. Processes that are coupled mainly through the variation of permeability as a function of stress may be treated with less tight coupling – and include reservoirs where the fluid compressibility is much higher than the rock compressibility (e.g. gas reservoirs). On the other hand, reservoirs that are poorly consolidated or scenarios involving thermal recovery methods (such as sands saturated with viscous oils) usually require fully coupled models as the pressure changes are strongly influenced by porosity changes.

During the course of simulation, a description of the recurrent data (well definitions, rates, shut-ins and flow-periods etc.) drives the computation process and estimates future values of various properties and parameters which change with time. These include pressures, saturations, temperatures, stresses, displacements etc. But before a coupled flow and geo-mechanical simulation can be run, the underlying static models need to be built. The static models are built on the basis of laboratory measurements as well as field data/experiments and require input from a variety of disciplines e.g., petrophysics, geology and geophysics. Thus, attributes derived from interpreted seismic data can be used in conjunction with tests conducted on core samples (e.g., UCS, tri-axial, direct shear) to build models of the expected geo-mechanical behaviour of rocks. Typical parameters used 32 CSEG RECORDER November 2011 Continued on Page 33 Coordinated by Kurt Wikel / Eric Anderson FOCUS ARTICLE November 2011 CSEG RECORDER 33 to define geo-mechanical models for coupled simulation include Young’s modulus, Poisson’s ratio, grain compressibility, coefficient of thermal expansion, cohesion and friction parameters, relationship between moduli and stress (e.g. linear, hyperbolic etc.), yield criteria (e.g. Drucker Prager, Mohr Coulomb etc.), and hysteresis. Current algorithms can handle arbitrary three-dimensional heterogeneity but the complexity of geo-mechanical models is often limited by sparsity of available data – and therefore layer-cake or simple stratified models are widely used.

While coupled geo-mechanical models present the rigorous approach to the complex and coupled physics, they often require data at the fundamental level which may be difficult to obtain, and even more difficult to populate the model with. For example, the permeability behaviour of a fractured rock is highly stress dependent (e.g., Sen and Settari, 2007) but its modeling requires the mechanical characterization of individual fractures as well as the definition of the joint sets in the reservoir. Similarly, the evolution of an enhanced permeability region during stimulation treatment (stimulated reservoir volume) which is of great interest for treatment optimization, can be modeled in principle as a dynamic development of shear fracturing using coupled models, but this technology is only just emerging (Nassir et al., 2009). All rigorously coupled methods are also computationally expensive and therefore there is a need for simpler practical approaches.

In the sub-surface, stress fields vary with depth and failure modes in reservoir materials can be best understood as functions of directional stresses. Therefore, the more computationally robust and accurate way to model the geo-mechanical behaviour of a reservoir requires a coupling between a flow module and a stress module. At each time-step of computation, reservoir pressures are converted to corresponding effective stress values and the permeability (and/or porosity) changes are determined as a function of effective stress. Thermal stresses that develop during a steam injection process can also be included in such calculations. Alternately, the use of pressure dependent permeability functions is a simple way to implicitly include geo-mechanical influences in flow models. These functions allow permeabilities to increase at high pressures (e.g. invasion of water during hydraulic fracturing) and allow for loss of permeability with depletion and fall in reservoir pressure (e.g. closure of microcracks and natural as well as induced fractures). Where justified, a similar dependence of porosity on pressure can also be included in conventional reservoir flow simulators. This approach does not require a separate and detailed geo-mechanical model to be coupled with flow computations, and can provide in some instances a good approximation to the coupled solution (e.g., when the reservoir deformation is essentially uni-axial, Sen and Settari, 2005). The approach is realistic but also avoids the geomechanical modeling of complex fractured media.

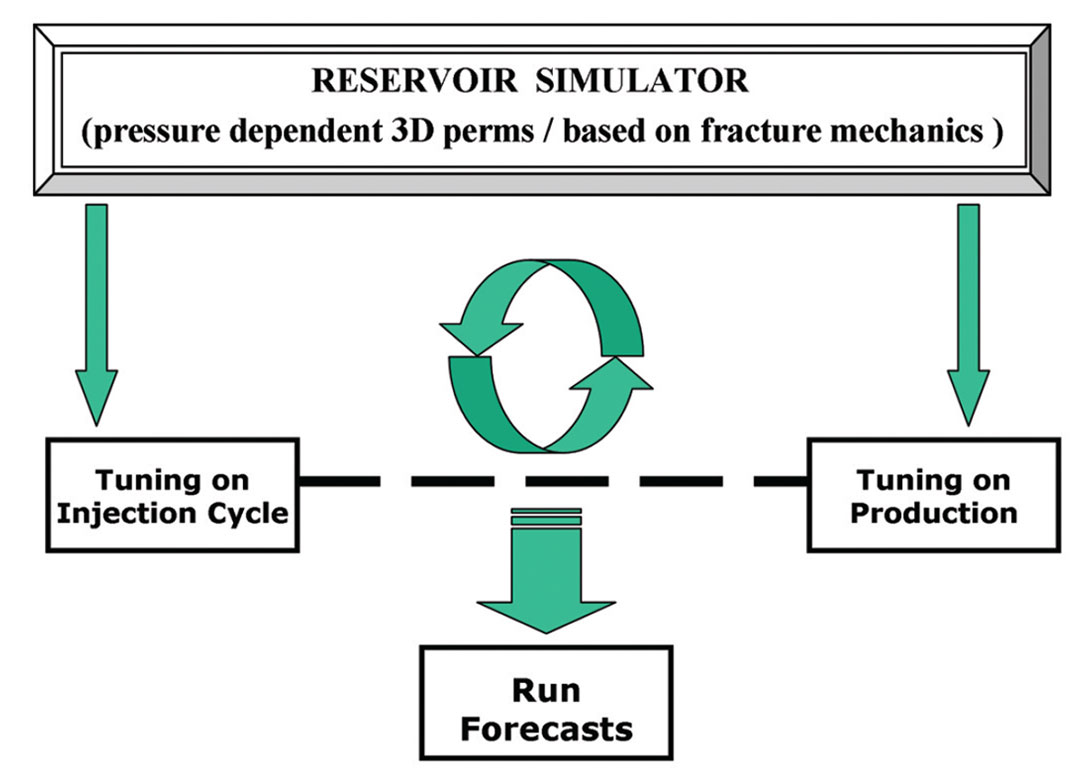
Modeling of Multi-stage Stimulation of Horizontal Wells

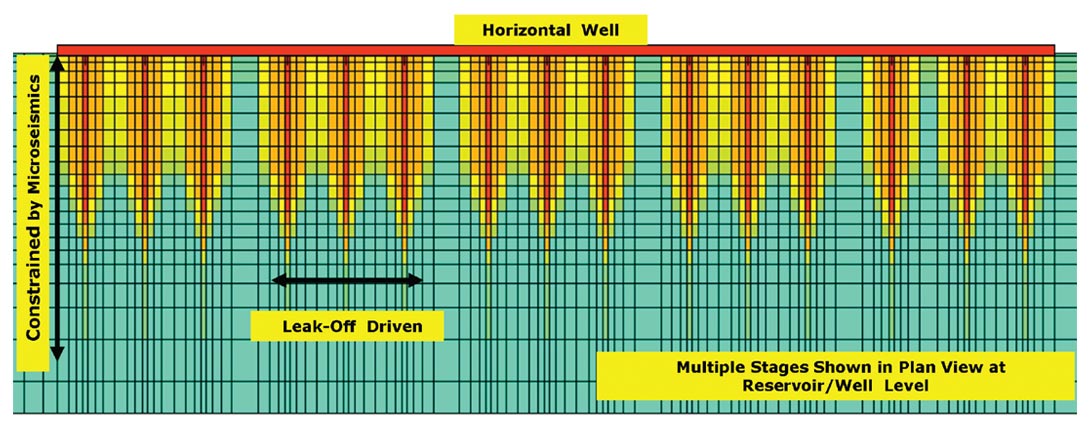
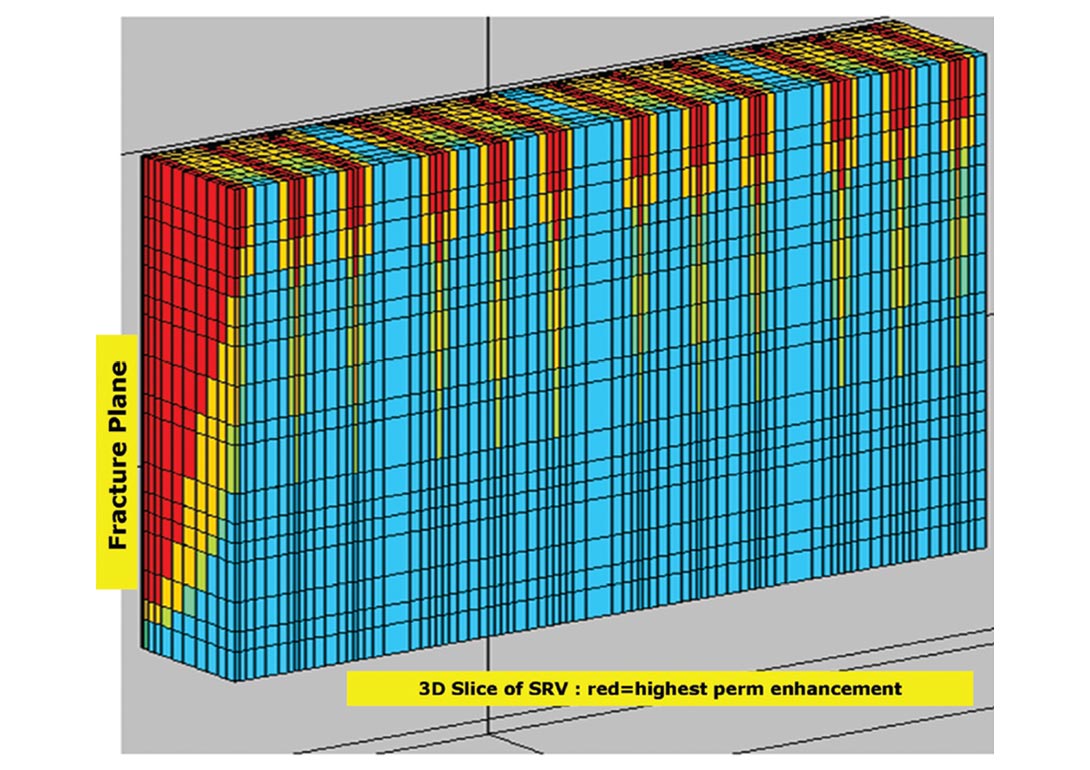
We recently investigated a two-step approach of this type where field data (either in the form of frac job parameters or historical production from stimulated wells) were used to refine a model of permeability dependence on pressure. At the same time, an estimate of a stimulated reservoir volume was dynamically computed as a function of injection rates, volumes and pressures. Well spacing (and stage spacing in horizontal wells) were changed and multiple injection/production configurations modeled to generate a cost-benefit matrix. The approach is directly applicable to the evaluation of hydraulic fracture stimulation of horizontal wells as well as thermal recovery programs. Figure 1 shows a schematic of the underlying concepts where a composite pressure (or stress dependent in case of coupling) permeability function is built as part of the reservoir flow model. The permeability function has a component for the propagating fracture planes and another for the leak-off into the surrounding rock matrix. The first part of a history-match involves modeling the hydraulic fracturing job. As an example, the pressures generated by pumping (and measured in the field) can be compared against modeled pressures and a match obtained by adjusting both permeability functions. Interpreted microseismic measurements may be used to constrain the maximum reach of the propagating fractures. Acting in tandem, the fracture and matrix permeability dependencies drive the growth of the stimulated reservoir volume, which can be estimated for different scenarios comprising different pump rates, volumes injected and stage configurations. Figure 2 shows a slice (in plan view) through a gridded stimulated reservoir zone that was estimated by a similar simulation. Several stages are represented along a horizontal well where fractures propagate from the perforations – extending out into the reservoir – and also enhance permeabilities through leak-off in the out-of-plane directions. The maximum fracture lengths were constrained by interpreted microseismic data for the actual well represented by this model. Figure 3 shows a 3D slice through the same stimulated volume and gives a different perspective. These figures show a permeability volume that was modified (from the initial static model) using coupled simulation and constrained by field observations (injection pressures). For a thermal recovery project, similar estimates can be made of the propagating stresses and thermal fronts. Where available, field measurements from probes and sensors can be used to constrain the models.

Once the stimulated zone has been modeled, the second part of the history match involves using the production history to further tune the permeability functions by modeling the loss of stimulated permeabilities with fall-off and depletion. Upon completion of the two-pronged exercise, the reservoir model – with geo-mechanics dependent permeability functions tuned and built-in – is ready for modeling various permutations of development plans. These will typically involve experimentation with well spacing (for pattern based development), number of frac stages, volumes to be pumped and pump rates. The production forecasts when assessed against expenses incurred for each development plan, will allow for NPV based evaluations and optimal plan selection.

Parting Thoughts

There are many other scenarios in reservoir appraisal and development where geomechanical effects must be given due consideration – where the suggestions offered in this paper are equally applicable. It is always prudent to start with a simple model (based on current understanding and supported by measurements and observations). One can progressively refine the model – over time – as long as the forecasts it generates continue to fall within a reasonable neighbourhood of actual occurrences.