Improving AVO fidelity by NMO stretching and offset dependent tuning corrections

Summary

Wavelet stretching due to NMO correction of seismic gathers causes problems in AVO. Coupled with the degrading action of wavelet stretching is offset dependent tuning for thin beds. Even though tuning is inherent in the data before NMO correction, its effect on AVO is more obvious on NMO corrected data. Studies have been carried out for an analytical understanding of NMO stretching and offset-dependent tuning and their correction to improve AVO fidelity. Based on these studies, we have implemented the NMO stretching and thin-bed tuning corrections in a practical fashion for production AVO analysis. Both synthetic and real data examples show that these corrections are necessary for performing reliable AVO analysis.

Introduction

Effects of normal moveout (NMO) on stacking and AVO analysis and their correction have been studied for over three decades. Dunkin and Levin (1973) were among the earliest who noticed that NMO procedure stretches wavelet waveforms, and they derived an analytical relationship to link spectral changes due to NMO correction and velocity and offset. Lin and Phair (1993), Swan (1997), and Dong (1999) attempt to quantify the effect of offset-dependent tuning on AVO and suggest solutions for correcting the AVO gradient, a commonly used indicator for hydrocarbon anomalies. Castoro et al (2001) analytically explain wavelet stretching and offset-dependent tuning and provide a practical procedure to correct them. More recently, researchers (Lazaratos and Finn, 2004, Roy et al, 2005, Perez and Marfurt, 2006) have focused their attention to the stretching effect during processing of data, as stretching and its resultant AVO biasing exist in the large incident angle data from depth migration. Lazaratos and Finn (2004) follow Dunkin and Levin (1973) and correct the stretching on the offset gathers by applying an inverse spectral shaping filter. Roy et al (2005) find an analytical derivation for wavelet stretching in migration depending only on reflection angle in the layered media. Perez and Marfurt (2006) seek a more robust implementation for correcting wavelet stretching after common-angle migration by combining the studies by Roy et al (2005) and Lazaratos and Finn (2004). Researchers have noticed the loss of high frequency at far offset after NMO correction, and deconvolution or spectral balancing is commonly used to compensate the high frequency loss.

When the offset range is limited to near offset for generating stack sections, the necessity of applying stretching and tuning corrections cannot be seen by many interpreters. However, when far offset data are used in the AVO analysis, stretching and tuning do bias observations. The out-of-phase AVO artifact due to stretching and tuning may generate artificial AVO anomalies and lower the reliability of AVO analysis. Based on the above-mentioned studies, we design and implement correction for wavelet stretching and offset-dependent tuning, and especially we use AVO inversion approach to compensate high frequency loss after NMO correction. Both synthetic and real data examples are used to test the effectiveness of the implementations. The real data example in this paper shows the necessity of applying stretching and tuning corrections prior to AVO analysis.

Method

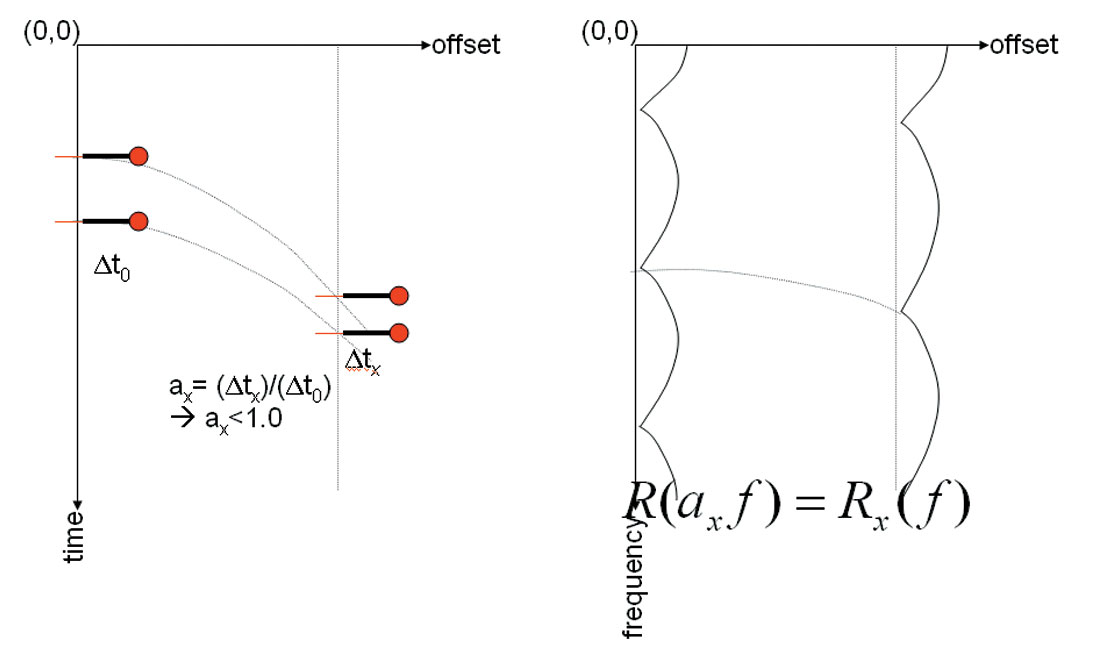
A short time segment of reflectivity at offset x can be regarded as a compressed version of corresponding normal incident reflectivity segment if velocity field variation is slow and AVO is neglected. The compression can be defined by a constant factor α_x. In frequency domain, R_x(f), spectrum of reflectivity at offset x, is the stretched version of that of the corresponding normal incident reflectivity segment, R(f):

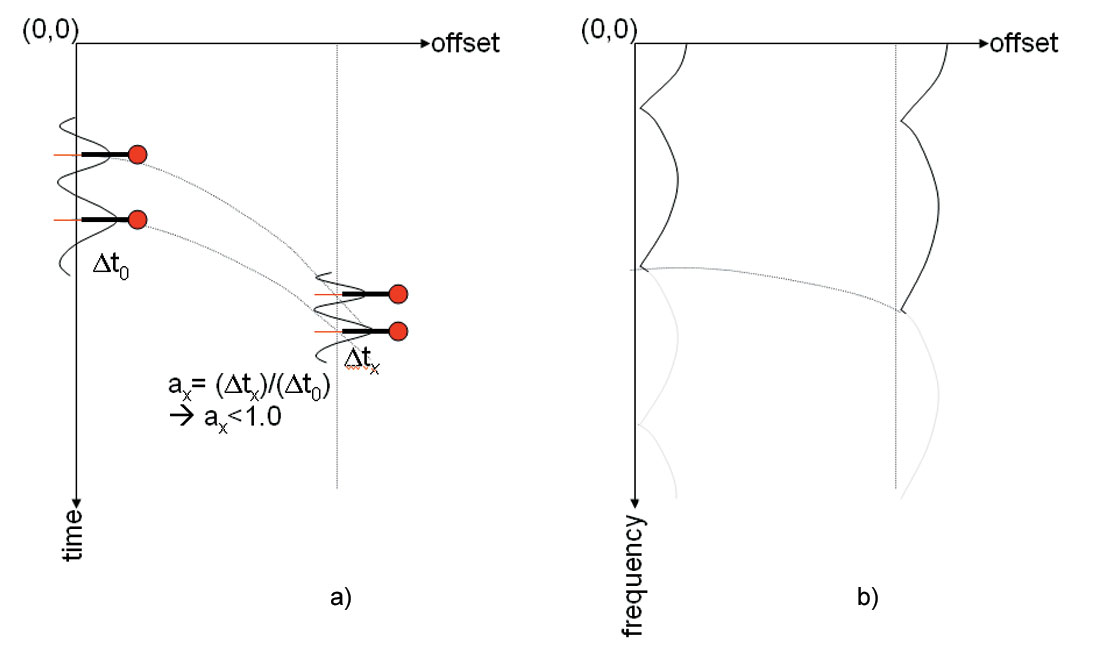
Equation (1) describes offset dependent tuning, which is illustrated by the diagram in Figure 1. As the spectrum of the tuned far offset traces is stretched, far offset traces need wider bandwidth than near offset traces to keep the same temporal resolution as illustrated by Figure 2. But for most of the surface seismic data, it is hard for far offset data to match the same bandwidth as near offset data, due to the stronger attenuation at far offsets than near offsets in terms of same reflection events and uniform bandpass filtering applied in the data processing.

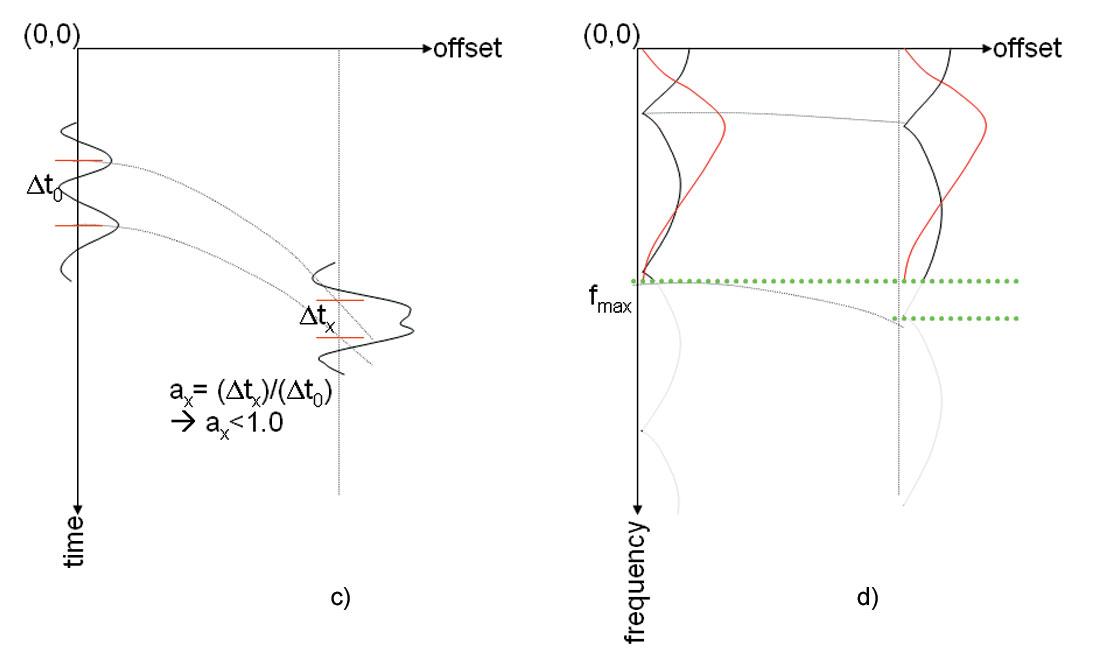
NMO correction removes the offset dependency of the timing in the reflectivity sequence. It stretches the reflectivity segments in time domain and squeezes the spectrum of frequency. The mathematical expression for NMO correction is

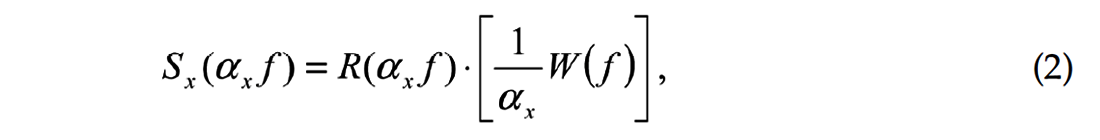
where S_x is the spectrum of reflectivity with wavelet after NMO correction, R is the reflectivity spectrum corresponding to zero offset traveling time, W is the spectrum of wavelet, and αx is the compression factor as in equation (1). Because α_x is usually a number less than 1, bandwidth is reduced after NMO correction, while the amplitude spectrum of the wavelet is amplified. The effect of NMO correction is illustrated in Figure 3.

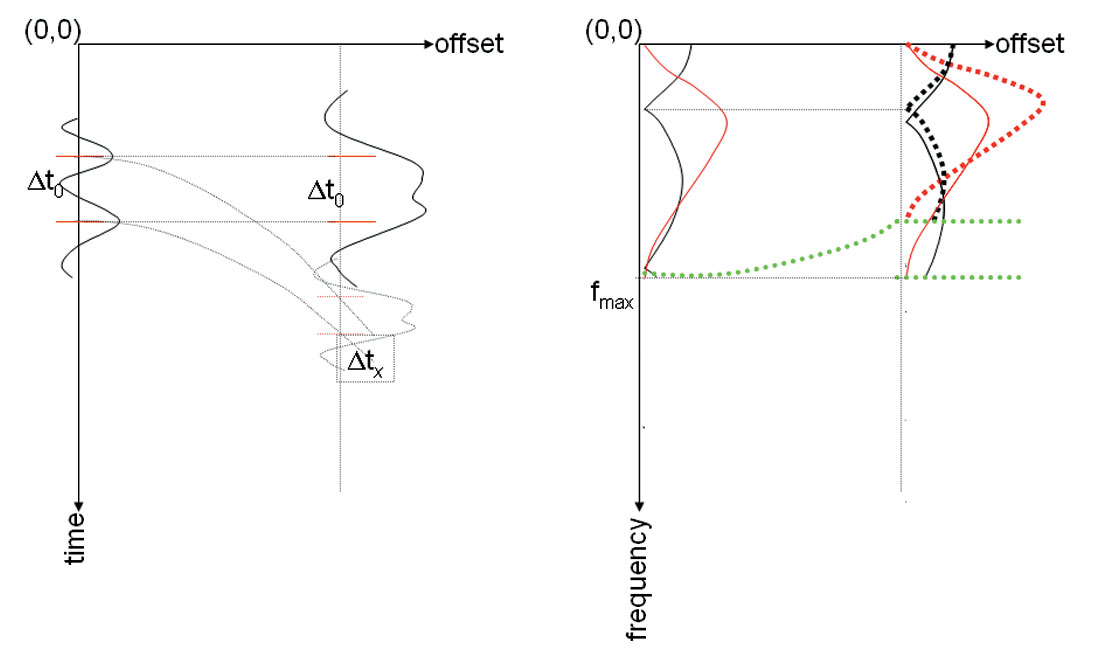
Based on the above discussion on the offset dependent tuning and NMO correction, we notice wavelet stretching and offset-dependent tuning corrections on the NMO corrected data should be done separately in the frequency domain. Wavelet stretching correction needs to be applied prior to tuning correction. For offset domain gather, if the time window is chosen small enough for mildly varying velocity field, stationarity assumption can be made (Castoro et al, 2001, Lazaratos and Finn, 2004). It is more practical to use overlapping time windows and averaging as suggested by Lazaratos and Finn (2004). Tests have to be done to look for optimal window size for stationarity assumption and computing efficiency. Wavelet stretching correction is based on the stretching factor given by Dunkin and Levin or Roy et al. It needs to be borne in mind that wavelet stretching correction can only reliably restore the usable frequency band at far offset, which is narrower than at zero offset trace. When the wavelet doesn’t have a box car spectral shape, wavelets need to be estimated first. Amplitude ratio of non-stretched wavelet to the stretched wavelet is used to scale the far offset data in frequency domain. This procedure was suggested by Castoro et al (2001). Compensation of high frequency loss due to tuning can not be correctly achieved by deconvolution or spectral balancing kind of approaches used by Castoro et al (2001), Roy et al (2005) and Lazaratos (2004). High frequency signal is usually missing or weak after NMO correction. Solution from deconvolution should be unstable. When AVO exists or time window is small, the spectrum is not white or spectral shape is difficult to predict. Here we suggest an approach to compensate high frequency loss at far offset by honoring AVO with the gather: the lost high frequency components at far offset can be estimated from near offset data, where the corresponding high frequency components exist. It is done by an AVO inversion approach. If the velocity field variation is mild and the chosen time window for analysis is small enough, the incident angle can be assumed as time-independent. The linear approximations of Zoeppritz equation in time domain have similar linear expression in frequency domain as the function of incident angle, and therefore AVO inversion can be performed on the frequency sample basis. The missing high frequency component at far offset can be modeled by using solution from AVO inversion. If wide range offsets lose their high frequency components, AVO inversion would be less reliable, and a local mud-rock line can be used to estimate a reasonable solution. In the absence of a reliable local mud-rock line, the ratio of AVO attributes, e.g. the intercept and gradient, can be estimated statistically from the reliable low frequency components in the analyzed time window after wavelet stretching correction.

Examples

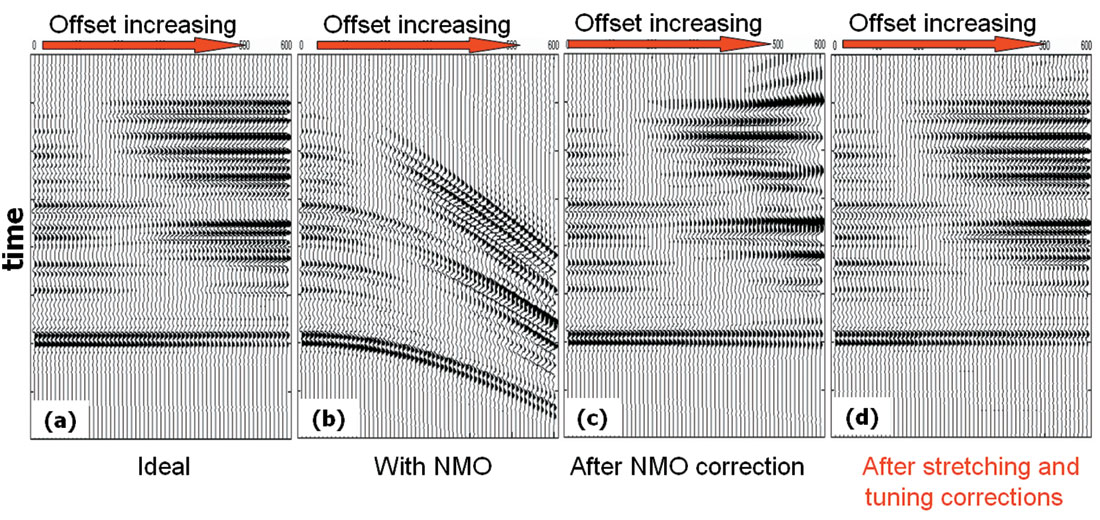
Figure 4 shows stretching and tuning correction on a synthetic gather with strong AVO. The useful signal zone is about 250ms and a single window is used to calculate the stretching factor. The gathers resulting from stretching and tuning corrections closely match the ideal gathers. More importantly, AVO distortion is fixed after the stretching and tuning corrections.

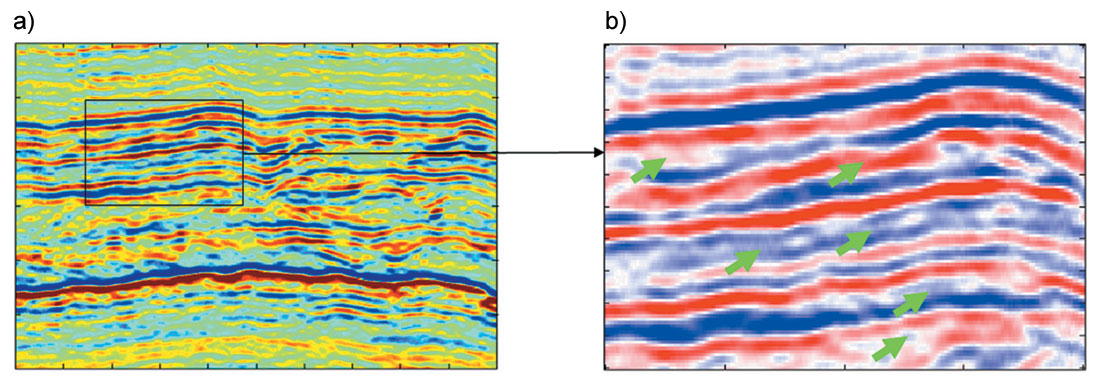
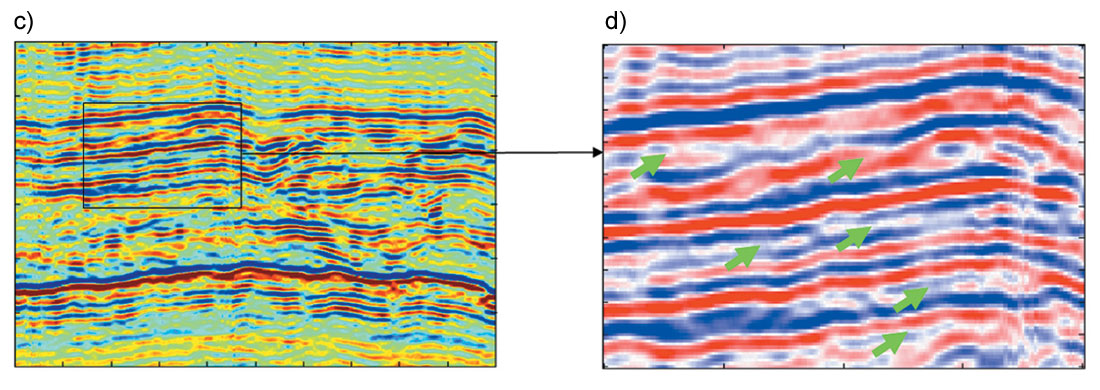
A real dataset from Alberta, Canada was used to test NMO stretching and offset-dependent tuning correction. Data was processed in an AVO friendly fashion and NMO correction was applied. The improvement of AVO fidelity by stretching and tuning corrections is shown in Figure 5 and Figure 6. Figure 5 shows an NMO corrected CDP gather to demonstrate the effectiveness of corrections. Note the high frequency loss at far offset due to offset-dependent tuning and the enrichment of low frequency at far offset due to NMO stretching in Figure 5 (c). The box in dotted line indicates the frequency band weakly affected by offset-dependent tuning. Black arrows indicate the gas reservoir top and red arrows indicates a reference event from Paleozoic unconformity. Figure 5 (b) shows the AVO modeling using the well with a gas reservoir at the location of this CDP gather. No NMO or offset dependent tuning is applied in the modeling. Amplitude increasing with offset at the reservoir top is obvious on the modeling while no obvious AVO increasing can be seen at the reservoir top on the real data; and there is no obvious amplitude changing at the geological marker on the modeling gather while amplitude increasing with offset is seen on the real data. Figure 5 (d) is the gather after band pass filter defined by the red dot-line box in (c). The gather in Figure 2 (e) is generated by applying NMO stretching correction only on the gather in Figure 2 (d). The amplitude increasing AVO on reference marker event (red arrow) is reduced. Figure 2 (e) shows the gathers after compensation of high frequency components on far offset traces. An increasing AVO can be seen clearly at the reservoir top indicated by the black arrow. The reference marker indicated by the red arrow shows little AVO, which matches AVO modeling.

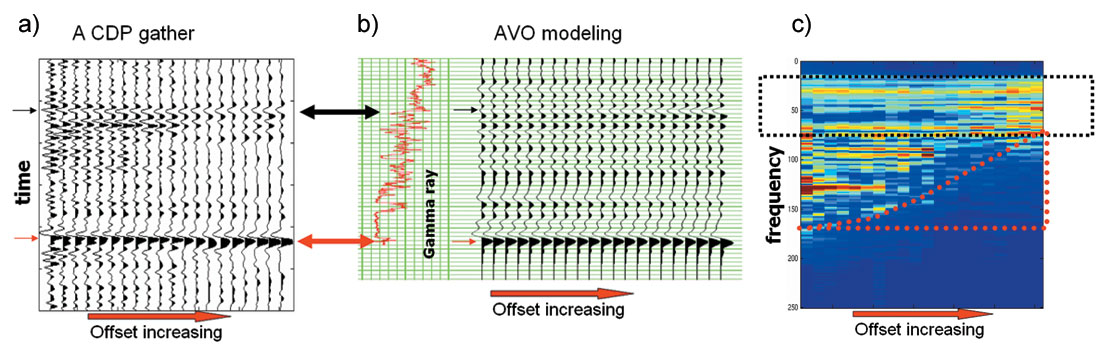
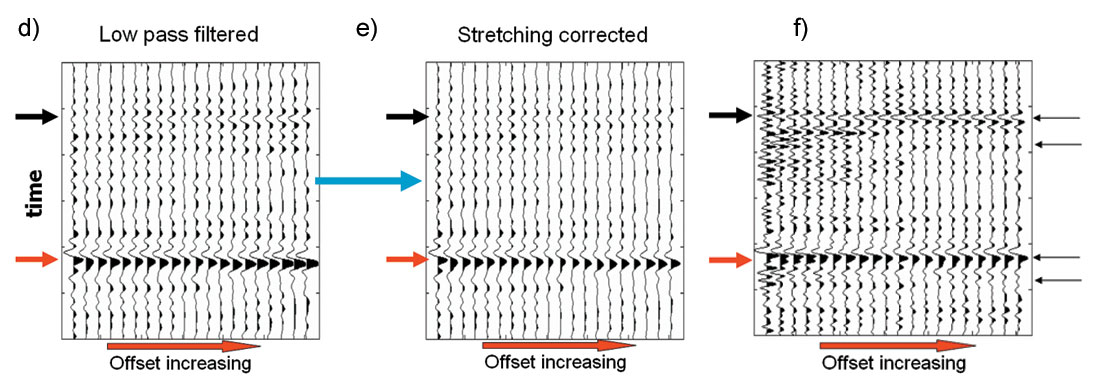
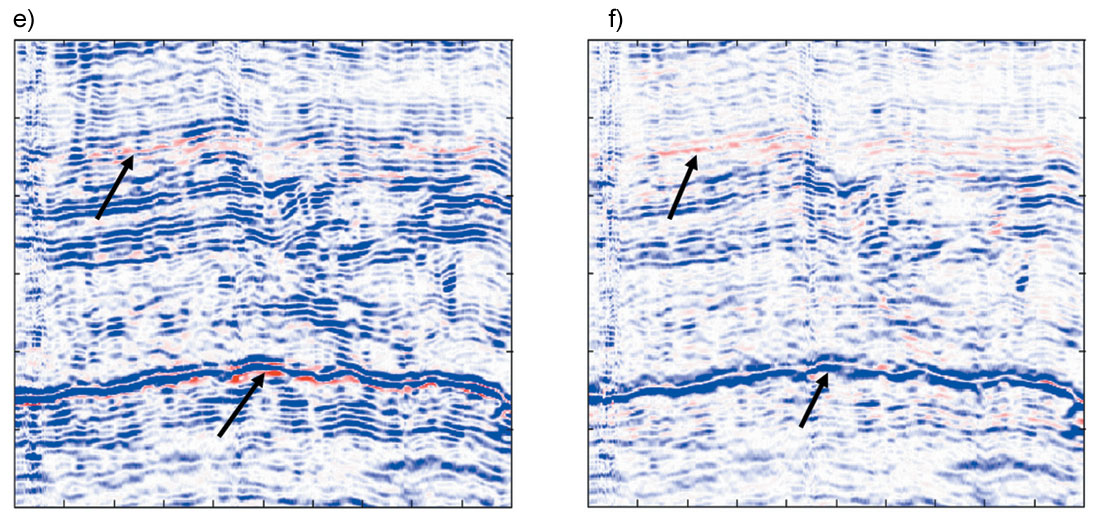
Figure 6 presents the stack sections and AVO attributes. Comparisons are made on the results from data with and without stretching and tuning corrections. Figures 6 (a) and 6 (c) compare the stack sections with and without stretching and tuning corrections. Figures 6 (b) and 6 (d) show an enlarged portion of them. Because tuning correction compensates the high frequency components for far offset traces, it enhances the resolution on the stack section. Black arrows on (b) and (d) indicate obvious resolution difference of them. The AVO intercept and gradient sections are extracted from the gathers with and without stretching and tuning corrections. The product of intercept and gradient can be used to indicate AVO anomalies. Figure 6 (e) shows the product of intercept and gradient without stretching and tuning corrections while the product of intercept and gradient from data with these corrections is displayed in Figure 3 (f). In (e) and (f), the black arrows indicate the reservoir target, and red arrow points to the Paleozoic unconformity marker. As a weak class III or Class II-b AVO, as seen in Figure 5 (f), is expected at the reservoir target, positive product (red color) of intercept and gradient should be seen at the reservoir zone while most of other portion of the section should have negative product value (blue color). Although the reservoir, indicated by black arrows, can be found on both (e) and (f), it is more consistent and standout on (f). The larger overall product value on (e) than on (f) can be explained by the fact that tuning generates larger gradient when thickness of thin layer is larger than 1/12 wavelength for dimming AVO (see the derivation by Lin and Phair, 1993). Obvious artifact anomalies can be seen on (e) at the geological marker indicated by the red arrows. This marker is on Paleozoic unconformity surface and has a strong impedance contrast and wavelet stretching generates strong out-of-phase side lobes, which generates artifact AVO anomaly. Stretching and tuning correction reasonably remove these artificial anomalies.

Conclusions

There are two main reasons for the loss of AVO fidelity in the NMO correction: one is low frequency amplification due to wavelet stretching, and the other one and also more important is the intrinsic loss of high frequencies due to filtering during wave propagation and processing for offset-dependent tuning events. The wavelet stretching can be restored by a relative deterministic approach, but the high frequency loss due to tuning and filtering we believe requires AVO guided frequency extrapolation in order to restore AVO. This study suggests a stretching and tuning correction procedure. The model and real data examples demonstrate the necessity of applying corrections for stretching and tuning for performing reliable AVO analysis. Improvement of AVO fidelity by stretching and tuning correction is m o re obvious for wide-angle AVO analysis and for the geological setting where the reservoir sits within a tight formation and beneath a lower impedance shale layer. The real data from Western Canadian Sedimentary Basin shown in the above section has approximated largest angle of 39 degrees and the application of stretching and tuning corrections on it provides more reliable AVO analysis results.